Introduction
The numbering system you and I use normally is called the decimal system, as it goes up in multiples of 10.
However, as we learnt in the last lesson, computers use the binary system, where numbers increase in multiples of 2.
It’s important that when learning binary, we know how to convert numbers between binary and decimal.
In this lesson, we’ll learn about:
- The difference between binary and decimal.
- How to convert decimal numbers to binary.
- How to convert binary numbers to decimal.
The Difference Between Binary & Decimal
Let’s think about the number 12.
It’s actually two separate numbers – 1 & 2. However, they belong to different columns.
| TENS | ONES |
|---|---|
| 1 | 2 |
The number 12 can be thought of as ONE TEN and TWO ONEs.
In the decimal system, each column goes up in multiples of 10. Each column can be given a value of 0-9 (10 possible values).
| TEN THOUSANDS | THOUSANDS | HUNDREDS | TENS | ONES |
|---|---|---|---|---|
| 0-9 | 0-9 | 0-9 | 0-9 | 0-9 |

The Difference Between Binary & Decimal
So, let’s look at the number 4096.
| THOUSANDS | HUNDREDS | TENS | ONES |
|---|---|---|---|
| 4 | 0 | 9 | 6 |
As you can see, we have:
- 4 thousands
- 0 hundreds
- 9 tens
- 6 ones
This should all be pretty familiar to you from primary school and key stage 3.

The Difference Between Binary & Decimal
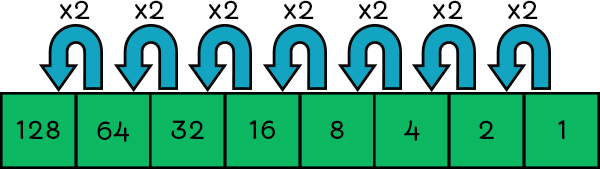
Binary numbers work very similarly, except the columns increase in multiples of two, and each column can only store a 0 or 1.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0-1 | 0-1 | 0-1 | 0-1 | 0-1 | 0-1 | 0-1 | 0-1 |
Notice how each column is simply a multiple of 2, as shown in figure 1.

The Difference Between Binary & Decimal
When working with binary, it is helpful that you get your columns drawn out first.
Remember, the smallest numbers are on the RIGHT, and the numbers go up by multiples of 2 RIGHT TO LEFT.
The smallest number in a binary sequence is known as the “least significant bit”.
The largest number is known as the “most significant bit”.
Before beginning any binary math, always write your numbers down in the right order – you can’t miss!

Converting Decimal to Binary
In order to cover decimal to binary, you need to ask yourself the following question:
Can I take away my binary column from my decimal number and be left with a positive?
Or
Can my binary column fit into my decimal number?
Let’s examine the decimal number 25 and convert it into a 6-bit binary number.
Firstly, we need to put our binary columns down. As it is going to be 6 bits, we need 6 columns:
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|

Converting Decimal to Binary
Step 1
Start with the 32 column (our most significant bit). Can 32 fit into 25?
No, so we don’t have any of these, so we put 0 in the 32 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 |
Step 2
Move onto the 16 column. Can 16 fit into 25?
Yes, so we have one of these, so we put 1 in the 16 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 | 1 |
Now we have to take 16 away from 25. 25 – 16 = 9.

Converting Decimal to Binary
Step 3
Move onto the 8 column. Can 8 fit into 9?
Yes, so we have one of these, so we put 1 in the 8 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 | 1 | 1 |
Now we have to take 8 away from 9. 9 – 8 = 1.
Step 4
Move onto the 4 column. Can 4 fit into 1?
No, so we don’t have one of these, so we put a 0 in the 4 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 |

Converting Decimal to Binary
Step 5
Move onto the 2 column. Can 2 fit into 1?
No, so we don’t have one of these, so we put a 0 in the 2 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 |
Step 6
Move onto the 1 column (our least significant bit). Can 1 fit into 1?
Yes, so we have one of these, so we put a 1 in the 1 column.
| 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 0 | 1 |
Now we have to take 1 away from 1. 1 – 1 = 0.
And our conversion is now finished!

Converting Decimal to Binary
Basically, you need to keep subtracting until you reach zero, and your final number MUST be either a 0 or a 1.
If you end up with anything other than 0 or 1, then your math has gone wrong.
So, the number 25 in the 6-bit binary is 011001, which is correct.
You must always give your answer in the required number of bits. Your exam will usually want your answer in 8 bits.
The number 25 in 8-bit binary is:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |

Converting Decimal to Binary
There’s one final thing to note when converting a decimal number to binary.
In decimal, if a number starts with a 0, it is usually ignored. For example, we never say, “I’ll have 05 bags of crisps”.
However, in binary, it is important that these are written down, as you will then use the required number of bits.

Converting Binary to Decimal
In order to convert from binary to decimal, we take our binary number and put it in the columns.
Let’s take the number 25 again. In a 6-bit binary, we saw that this was 011001.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
To convert this back into decimals, we need to work out which columns have a ONE in them.
| 16 | 8 | 1 |
|---|---|---|
| 1 | 1 | 1 |
Then, we simply need to add up these column heading values: 16+8+1=25.
And that’s all it takes.

Converting Binary to Decimal
This works for any number. For example:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Pick all the 1’s.
| 128 | 32 | 16 | 8 | 2 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
Add them up.
128+32+16+8+2=186.

Lesson Summary
The decimal number system is based on a counting system where columns go up by multiples of 10.
The binary number system is based on a counting system where columns go up by multiples of 2.
To convert decimal to binary keep taking away until you reach zero.
To convert binary to decimal, add up all the binary columns that contain a 1.
When converting decimal to binary you should only have a 1 or a 0 in each column.

